最近論文を読んでいて因果関係と相関関係に関して考えることがあり、色々調べました。まとめたいと思います。
因果関係？
今回私が読んだ論文は重回帰分析という手法を使ってデータの統計処理をしていました。複数の因子を同時に比較する手法で、最終的には相関係数の数値を基にデータの価値（関係の強さ）を判断することになります。一般的に言われている基準は、
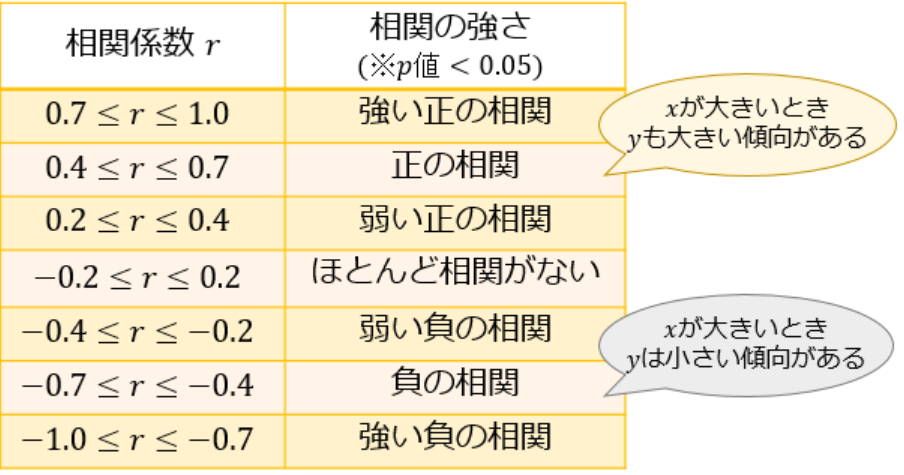
今回の相関係数0.49は「めちゃくちゃ高いわけじゃないけど、何か関係がありそう」逆に言うと「相関があるからと言って因果があるわけではない。」とも言えます。「何か関係がありそう」というのが相関関係です。因果関係にとって相関関係は必要不可欠ですが、その逆は言えません。
因果関係でなければいけないのか。
教育学においては、一卵性双生児を数組集め実証実験を行い因果関係を調べる手法がしばしば取られているそうです。しかし、スポーツ科学においてはすべての実験を双子で行うにはコストがかかり過ぎます。これだけ多くの研究結果が発表されているにもかかわらず、トレーニングによって体にどのような変化が起きているのか、詳細には分かっていません。そのため、相関を調べることの意義・重要性は間違いなくあります。ただ気を付けなくてはいけないのは、一つの実験を通して得られた結果に左右されてはいけません。複数の相関関係を複合的に考えて真実に近づき最後に判断する。相関関係のデータを取り扱うときには「それ以上でもなくそれ以下でもない」というスタンスが必要なのではと個人的には感じています。
因果関係の向き
また、大事な考え方として「因果関係の向き」という要素があります。
例えば、「殺人事件を起こした犯人は暴力的なシーンを含むゲームをしている時間が長い」という関係があった際に、そのようなゲームをさせてはいけないとする社会の風潮は日ごろから良く感じます。しかし、「殺人事件を犯すような暴力性を持ち合わせている人間が好んで暴力的なゲームをする」という逆向きの関係もあるわけです。この場合に実際の向きがどちらかを担保するものはありません。「統計学が最強の学問である」の著者、西内さんの言葉を借りるのであれあば「2つの集団が同じ条件ではない。フェアじゃない」です。
天才数学者フィッシャーの解決法
それでは、統計によって因果関係を示すことは不可能なのか。1930年代に活躍した数学者フィッシャーが発明した統計的手法が「ランダム化比較研究」です。データを取る段階で2つの群を作り、できるだけフェアな条件を揃え（バイアスを減らす）実験をする。この手法を取らない限り因果関係を示すことは非常に難しくなります。
このランダム化比較研究の強力なのは、因果関係を示すだけではなく様々な学問に応用可能だということです。当然スポーツ科学においても数多くの研究がこの手法を用いて実証実験を行っています。
「ビックデータ」という言葉が取りざたされ、私たちは普段から統計的な数値にさらされているわけですが、その数値にどれだけの意味があるのかを知らないと判断を惑わされてしまうでしょう。今後のITの社会で必要なリテラシーだと思います。西内さんの著書は難しい統計の世界をかなり分かりやすく書いて下さています。おススメです。
引用
西内啓著 統計学が最強の学問である
今日の一日一新
・メルカリ出品、買取
・あるオンラインコンサルタントに応募
今日の子供日記
・長女の姫ぶりにどう対処するか悩んでいます。時間が解決するのか、何か介入すべきか。ただ叱っているだけでは解決しなさそうです。
・長男は「ヤ！ハ！」と何かと戦うようになってきました。どらえもんは「ダエモン！」と発音してます。
・次女は最近市販のミルクをよく飲むようになりました。母乳が出にくくなるというデメリットもあるそうです。
コメント